Solve Complex Scientific Problems with SplitFXM

A powerful 1D computational physics library using Finite-Difference and Finite-Volume methods with asymmetric stencils and adaptive mesh refinement.

View on GitHub Learn More

Powerful Features

SplitFXM provides a comprehensive toolkit for tackling the most challenging computational physics problems.

Finite-Difference & Finite-Volume

Powerful numerical methods for solving differential equations with high accuracy.

Asymmetric Stencils

Flexible stencil configurations for handling complex boundary conditions and irregular domains.

Adaptive Mesh Refinement

Dynamically adjusts the computational grid to focus resources where they're needed most.

Newton & Split-Newton Solvers

Robust approaches for steady-state solutions of complex non-linear systems.

Handles Steep Gradients

Specially designed to capture sharp transitions in physical properties efficiently.

Multiple Boundary Conditions

Support for diverse boundary specifications to model real-world scenarios accurately.

Solver Comparison

How SplitFXM differs from traditional boundary value problem solvers?

SciPy's `solve_bvp` and Julia's `DifferentialEquations.jl`

Requires transformation of higher-order differential equations into first-order systems:

# Must convert to dy/dx = f(x,y,p) form
# Original equation: y'' + p*y' + q*y = g(x)
# Converted system:
# y1' = y2
# y2'  = g(x) - q*y1 - p*y2

Explicit Jacobian matrices must be provided for computationally intensive problems:

# Must define df/dy and df/dp manually
# This becomes increasingly complex for large systems

SplitFXM Approach

Work directly with governing equations in their natural form:

# Define equations as they appear in physics/engineering
# No need to transform to first-order systems
# res = d2x(y) + p*dx(y) + q*y - g(x)

Sparse Jacobians at runtime - Enhanced performance for complex systems

Comparison

For the Blasius Problem (η_max = 10, N = 100)

Method	Time (s)
SplitFXM++	~0.065
SciPy solve_bvp (no Jacobian)	~0.073

By focusing on the natural form of equations, SplitFXM makes it more intuitive and accessible while providing computational efficiency.

The “Split” Methodology

Our unique approach divides complex systems into multiple variable segments for more efficient computation.

1. System Division

Break down complex physical systems into manageable subsystems.

2. Variable Fixing

Hold some variables fixed while solving for others in each subsystem.

3. Iterative Solution

Alternate between subsystem solutions, gradually converging to the complete system solution.

4. Recursive Processing

Apply the same approach recursively for highly complex systems.

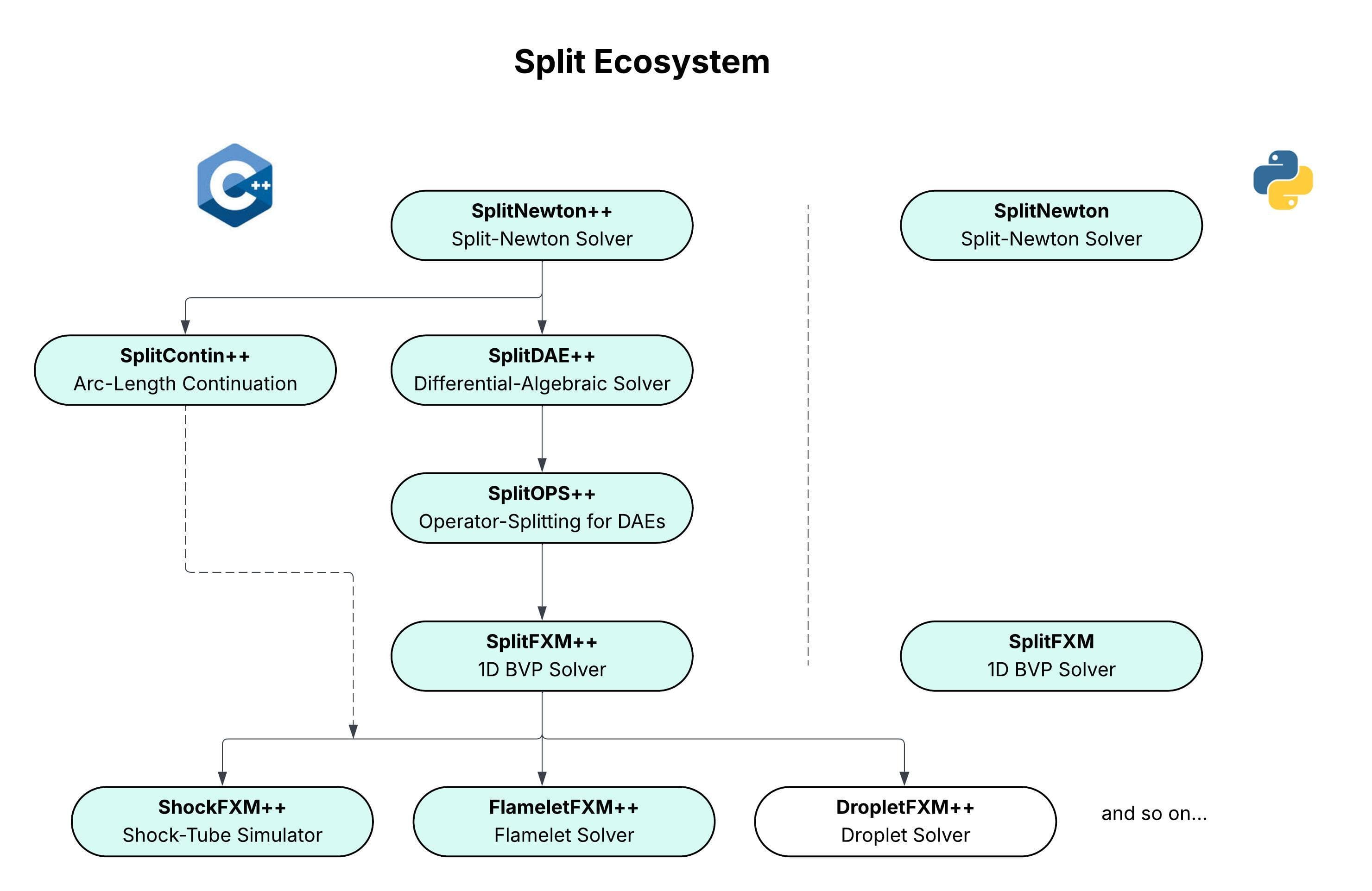
“Divide and conquer for complex numerical solutions”

Examples

Check out an example application for shock-tube simulation - ShockFXM++

Interested in a state-of-the-art flamelet solver? Contact us

Application Domains

SplitFXM excels at solving challenging 1D problems across multiple scientific disciplines.

🌬️ Compressible Flows

Model gas dynamics, shock waves, and acoustics with precision.

🔥 Combustion

Simulate complex reactions and heat release in combustion processes.

🔋 Batteries

Analyze electric potential distribution and ion transport in battery cells.

❄️ Phase Changes

Track interfaces and property jumps during phase transformations.

🌡️ Heat Transfer

Model conduction, convection, and radiation heat transfer mechanisms.

⚗️ Chemical Kinetics

Solve stiff reaction networks with numerous species and reactions.

⚡ Plasma Physics

Simulate ionized gas behavior under electromagnetic influences.

🧲 Magnetohydrodynamics

Couple fluid flow with electromagnetic fields for complex plasma models.

Pricing

Simple and transparent licensing options

License Type	Price	Intended Use	Action
Non-Commercial	Free	Research, educational, and personal use	Download
Commercial	On Request	Business purposes or revenue-generating use	Request
C++ Version (including pre-requisites)	On Request	For all purposes	Request

Non-commercial use is licensed under Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0)

Have questions? Contact us

Citing SplitFXM

If you use SplitFXM in your research, please cite it using the following format:

@software{pavan_b_govindaraju_2025_14827049,
  author       = {Pavan B Govindaraju},
  title        = {gpavanb1/SplitFXM: v0.5.0},
  month        = feb,
  year         = 2025,
  publisher    = {Zenodo},
  version      = {v0.5.0},
  doi          = {10.5281/zenodo.14827049},
  url          = {https://doi.org/10.5281/zenodo.14827049},
}

SplitFXM is an open-source project. Your acknowledgment helps support its continued development.

Star on GitHub View DOI